十字交叉法原理 十字交叉法的数学原理
1、原理：混合前，整体一，数量x，指标量a整体二，数量y，指标量b（a>b）混合后整体，数量（x+y），指标量c可得到如下关系式：x×a+y×b=（x+y）c推出：x×（a-c）=y×（c-b）得到公式：（a-c）：（c-b）=y：x则任意知道x、y、a、b、c中的四个，可以求出未知量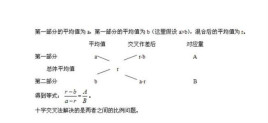
不过，求c的话，直接计算更为简单。当知道x+y时，x或y任意知道一个也可采用此法；知道x：y也可以。
2、十字交叉法的本质就是解二元一次方程的简便形式，该类题目也可以列方程解，使用该法则的具体方法如下：像A的密度为10，B的密度为8，它们的混合物密度为9，你就可以把9放在中间，把10和8写在左边，标上AB，然后分别减去9，可得右边分别为1和1。此时之比就为1:1 。
数学十字交叉法原理如何解析?
“十字交叉法”是中学化学计算中常用的解题方法，尤其是在一些不要求计算过程的选择型和填空型计算题的解答中使用十分方便。但交叉后的比例关系所代表的含义对许多同学来说是一个盲点，只有明确了“十字交叉法”的原理，才能迅速解题。
一、“十字交叉法”的数学原理
物理量可分为两类：一类物理量不具有加和性，如密度、浓度、摩尔质量等，这类物理量称为“强度量”；另一类物理量则具有加和性，如质量、体积、物质的量等，这类物理量称为“广度量”。
某混合物由两组分混合而成，设a1、a2(a1>a2)分别为两组分的某强度量，a为混合物的某强度量，x1、x2分别为混合物中两组分的某广度量，若满足下列方程式：a1x1+a2x2=a(x1+x2)，可知x1(a1-a)=x2(a-a2)，则=（即混合物中两组分某广度量之比）。
凡满足上述方程式的量都可以用“十字交叉法”表示如下：
a1 a-a2 x1
a =
a2 a1-a x2
【例题】H2和NH3形成的混合气体，其平均摩尔质量为14·mol-1，求H2和NH3的物质的量之比。
【解析】（1）用“数学法”求解：
设H2的物质的量为x1mol，NH3的物质的量为x2mol，则：2x1+17x2=14(x1+x2)，解得：。
（2）用“十字交叉法”求解：
2 3 1 x1
14 = =
17 12 4 x2
二、“十字交叉法”所求比值的含义——“看分母法则”
当我们明确了“十字交叉法”的数学原理后，很自然地会产生这样的疑问：上述广度量的比值（即）代表什么含义？与强度量有何关系？解决这个问题是我们正确使用“十字交叉法”的关键。由于存在“强度量×广度量”，可知广度量的含义与强度量的物理意义有关。
例如，摩尔质量这个强度量等于物质的质量除以该物质的物质的量，则其对应的广度量应为物质的量，也就是摩尔质量这个强度量的分母所表示的物理量，十字交叉后的比值为两组分的物质的量之比（如上述例题）。
由以上可知：十字交叉后的比例关系为该强度量的分母所表示的广度量之比。
化学十字交叉法原理是什么 化学十字交叉法原理是怎样的
1、十字交叉法的原理：A×a%+B×b%=(A+B)×c% 整理变形得:
A/B=(c-b)/(a-c ) ①
如果我们以100g溶液所含的溶质为基准，上式表示溶液混合时它们的质量比与有关质量分数比的关系。
可得如下十字交叉形式
a c-b
c
b a-c ②
对比①、②两式可以看出：十字交叉关系中(c-b)/(a-c)为组分A和组分B混合时的质量比，推广到二组分混合体系中，当以一定质量的混合体系为基准所得十字交叉关系，其比值为质量比（例如质量分数是以质量为基准）；若有c-b比a-c的化学意义由平均值c决定，则比值就表示组分A中c-b和组分B中a-c所表示的量的比值。如c为质量或质量分数，则(c-b)/(a-c)表示组分A和组分B溶液的质量之比；若c为密度，则(c-b)/(a-c)就表示组分A和组分B的溶液体积之比；若c为摩尔质量，则(c-b)/(a-c) 就表示组分A和组分B的物质的量比。此时可用十字交叉法求混合物中各组分的含量。
2、十字交叉法可用于溶液浓度的计算，例如溶液的稀释、浓缩或混合等计算题。使用此法，使解题过程简便、快速、正确。下面通过例题介绍十字交叉法的原理。
十字交叉法原理是什么？
十字交叉法原理就是一种二元一次方程的解法，具体如下：
x + y = 1
ax + by = c
c介于a与b之间，求解：x：y。
扩展资料
十字交叉法常用于求算：
（1）有关质量分数的计算。
（2）有关平均相对分子质量的计算。
（3）有关平均相对原子质量的计算。
（4）有关平均分子式的计算。
（5）有关反应热的计算。
（6）有关混合物反应的计算。
