一、小数是有理数还是无理数
答:小数可以是有理数,也可以是无理数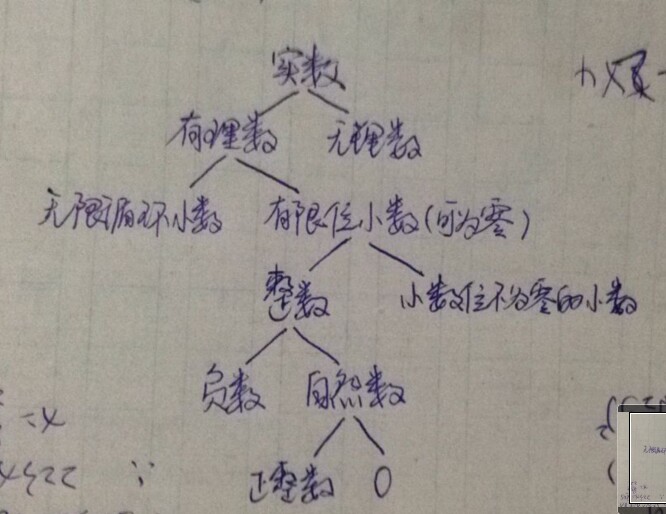
分析:
实数可以分为整数和小数,整数都是有理数。
小数又分为有限小数和无限小数,有限小数也都是有理数。
无限小数又可分为无限循环小数和无限不循环小数,其中无限循环小数也是有理数,无限不循环小数是无理数。
综上所述,在所有实数中,只有无限不循环小数才是无理数,其他都是有理数。
如:
3、5.5555......(5循环)都是有理数;而3.14159……(不循环)是无理数。
二、小数是有理数吗
小数是有理数。
有理数是整数和分数的统称,一切有理数都可以写成分数的形式。
小数分为两类,一种是有限小数,一种是无限小数;有限小数如0.25、6.25等,这些也可以写成分数的形式,所以有限小数是有理数;而无限小数又分为两种,一种是无限循环小数,一种是无限不循环小数;无限循环小数如0.3181818……可以写为7/22,所以无限循环小数是有理数。
相关内容:
有理数集与整数集的一个重要区别是,有理数集是稠密的,而整数集是密集的。将有理数依大小顺序排定后,任何两个有理数之间必定还存在其他的有理数,这就是稠密性。整数集没有这一特性,两个相邻的整数之间就没有其他的整数了。
有理数是实数的紧密子集:每个实数都有任意接近的有理数。一个相关的性质是,仅有理数可化为有限连分数。依照它们的序列,有理数具有一个序拓扑。有理数是实数的(稠密)子集,因此它同时具有一个子空间拓扑。
三、小数是不是有理数
小数是有理数。
有理数是整数和分数的统称,一切有理数都可以写成分数的形式。
小数分为两类,一种是有限小数,一种是无限小数;有限小数如0.25、6.25等,这些也可以写成分数的形式,所以有限小数是有理数;而无限小数又分为两种,一种是无限循环小数,一种是无限不循环小数;无限循环小数如0.3181818……可以写为7/22,所以无限循环小数是有理数。
相关内容:
有理数集与整数集的一个重要区别是,有理数集是稠密的,而整数集是密集的。将有理数依大小顺序排定后,任何两个有理数之间必定还存在其他的有理数,这就是稠密性。整数集没有这一特性,两个相邻的整数之间就没有其他的整数了。
有理数是实数的紧密子集:每个实数都有任意接近的有理数。一个相关的性质是,仅有理数可化为有限连分数。依照它们的序列,有理数具有一个序拓扑。有理数是实数的(稠密)子集,因此它同时具有一个子空间拓扑。
四、小数是有理数吗为什么
有限小数和无限循环小数是有理数;无限不循环小数不是有理数,是无理数。有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合。小数,是实数的一种特殊的表现形式。
有理数
整数也可看做是分母为一的分数。不是有理数的实数称为无理数,即无理数的小数部分是无限不循环的数。是“数与代数”领域中的重要内容之一,在现实生活中有广泛的应用,是继续学习实数、代数式、方程、不等式、直角坐标系、函数、统计等数学内容以及相关学科知识的基础。
有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数,有理数集与有理数是两个不同的概念。有理数集是元素为全体有理数的集合,而有理数则为有理数集中的所有元素。
小数
所有分数都可以表示成小数,小数中的圆点叫做小数点,它是一个小数的整数部分和小数部分的分界号。其中整数部分是零的小数叫做纯小数,整数部分不是零的小数叫做带小数。