一、斯托克斯定律的主要作用
该定律由乔治·斯托克(1819.08.13—1903.02.01)发现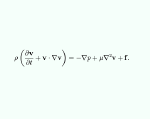
斯托克斯定律是颗粒半径与颗粒在静水中自由沉降速率的关系式。
斯托克斯公式是格林公式的推广。
利用斯托克斯公式可计算曲线积分。
球形物体在流体中运动所受到的阻力,等于该球形物体的半径、速度、流体的黏度与6π的乘积。这个定律叫做斯托克斯定律。如果物体在流体中因自身的重量而下落,根据上面公式,则为最终速度。
实验表明:黏滞阻力的大小与物体的形状,速度,流体的黏滞系数等有关。对半径为r的小球,在黏滞系数为
η的流体中以速度v运动时受到的黏滞阻力为:f=6πηrν,该式被称为斯托克斯定律,或斯托克斯公式。该式可用来测定流体的黏滞系数和微小颗粒的半径。
二、斯托克斯公式的应用条件是什么?
条件:当曲面是面xOy上的一块平面闭区域时
斯托克斯公式建立了沿曲面 S 的曲面积分与沿 S的边界曲线 L 的曲线积分之间的联系.
对曲面 S 的侧与其边界曲线 L 的方向作如下规定:设人站在曲面 S 上的指定一侧,沿边界曲线 L 行走,指定的侧总在人的左方,则人前进的方向为边界曲线L 的正向.这个规定方法也称为右手法则。
扩展资料
纳维-斯托克斯方程在建模仿真中的应用
纳维-斯托克斯方程是流体流动建模的核心。在特定的边界条件(如入口、出口和壁)下求解这些方程,可以预测给定几何体中的流体速度和压力。
由于这些方程本身的复杂性,我们只能得到非常有限的解析解。例如,对于两个平行板之间的流动或圆管内的流动,方程的求解会相对容易一些;但对于更为复杂的几何结构,求解方程会非常困难。
参考资料来源:百度百科-斯托克斯公式
三、斯托克斯定律 斯托克斯定律的解释
1、斯托克斯定理斯托克斯定理(英文:Stokes theorem)是微分几何中关于微分形式的积分的一个命题,它一般化了向量微积分的几个定理,以斯托克斯爵士命名。
2、当封闭周线内有涡束时,则沿封闭周线的速度环量等于该封闭周线内所有涡束的涡通量之和,这就是斯托克斯定理。
3、斯托克斯定理表明,沿封闭曲线L的速度环量等于穿过以该曲线为周界的任意曲面的涡通量。
四、什么是斯托克斯数
斯托克斯数(Stokes number)是一个无量纲数,颗粒松弛时间和流体特征时间的比,它描述了悬浮颗粒在流体中的行为。
目录
斯托克斯数
斯托克斯数(Stokes number)是一个无量纲数,颗粒松弛时间和流体特征时间的比,它描述了悬浮颗粒在流体中的行为。
中文名
斯托克斯数
外文名
Stokes number
Stk=τ*uo/dc
τ 是颗粒的弛豫时间,
uo 是液体通过障碍物时的流速,
dc是障碍物的特征量
当Stk>1时,当流线绕过障碍物时,颗粒会依然按直线行驶,直至撞上障碍物。
当Stk≤1时,颗粒会紧紧随着流线行驶。
物理意义:表征着颗粒惯性作用和扩散作用的比值,它的值越小,颗粒惯性越小,越容易跟随流体运动,其扩散作用就越明显;反之,值越大,颗粒惯性越大,颗粒运动的跟随性越不明显。
五、stocks 定律
Stokes’law(斯托克斯定律):
预测圆球在粘性介质中运动的摩擦力F的定律。根据这一定律,F=6πrηv,式中r为球半径,v为速度,η为介质的粘度。球加速直至到达一稳定终速为止。对于下落的球,F等于作用于球的重力。该定律由乔治·斯托克(1819—1903年)发现。
六、斯托克斯定理的介绍
斯托克斯定理(英文:Stokes theorem)是微分几何中关于微分形式的积分的一个命题,它一般化了向量微积分的几个定理,以斯托克斯爵士命名。