一、双曲线的实轴和虚轴是什么.....
实轴
两顶点之间的距离称为双曲线的实轴,实轴长的一半称为实半轴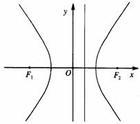
虚轴
在标准方程中令x=0,得y²=-b²,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴.
如上图中:
双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。
高中数学中的双曲线定义::
平面内,到两个定点的距离之差的绝对值为常数(小于这两个定点间的距离)的点的轨迹称为双曲线。
解析式如下:
标准方程为:
1、焦点在X轴上时为:
(a>0,b>0)
2、焦点在Y 轴上时为:
(a>0,b>0)
拓展:
双曲线的重要要素之渐近线
渐近线
双曲线有两条渐近线。渐近线和双曲线不相交。
渐近线的方程求法是:将右边的常数设为0,即可用解二元二次的方法求出渐近线的解,例如:
,将1替换为0,得,则双曲线的渐近线为
一般地我们把直线
叫做双曲线(焦点在X轴上)的渐近线(asymptote to the hyperbola )
焦点在y轴上的双曲线的渐近线为
参考资料:
双曲线 百度百科
二、双曲线的实轴和虚轴分别是什么?
双曲线中实轴是2a,虚轴是2b。若为焦点在x轴上的双曲线,在x轴上的两焦点之间的距离长等于2a,也就是是双曲线的实轴,是双曲线两支中相距最近的点,相对应的2b就是虚轴,实轴长是指到定点的距离差为定长的常数,它的一半就是指所谓的表达式中的a,而虚轴长没有什么实际意义,往往和实轴一起用来讨论渐进线,它的一半就是所谓的表达式中的b。
双曲线的内容
在数学中,双曲线,多重双曲线或双曲线是位于平面中的一种平滑曲线,由其几何特性或其解决方案组合的方程定义,双曲线有两片,称为连接的组件或分支,它们是彼此的镜像,类似于两个无限弓,双曲线是由平面和双锥相交形成的三种圆锥截面之一,其他圆锥部分是抛物线和椭圆,圆是椭圆的特殊情况如果平面与双锥的两半相交,但不通过锥体的顶点,则圆锥曲线是双曲线。
它还可以定义为与两个固定的点,叫做焦点的距离差是常数的点的轨迹,这个固定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离,a还叫做双曲线的实半轴。焦点位于贯穿轴上,它们的中间点叫做中心,中心一般位于原点处。
三、双曲线虚轴是什么 双曲线中实轴和虚轴分别代表什么
1、双曲线中实轴等于2a,虚轴等于2b。
2、若为焦点在x轴上的双曲线,在x轴上的两焦点之间的距离长等于2a,也就是是双曲线的实轴,是双曲线两支中相距最近的点,相对应的2b就是虚轴。
3、实轴长是指到定点的距离差为定长的常数,它的一半就是指所谓的表达式中的a,而虚轴长没有什么实际意义,往往和实轴一起用来讨论渐进线,它的一半就是所谓的表达式中的b。
四、双曲线的实轴和虚轴是什么?
双曲线的实轴和虚轴分别是:X轴为实轴,y轴为虚轴。
两顶点之间的线段称为双曲线的实轴,实轴长的一半称为半实轴,实轴的长度为2a(a为标准方程中的参数)。在标准方程中令x=0,得y=-b,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴。
把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a,小于|F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线。
学好几何的方法
1、使用教具,小学生的思维能力、逻辑能力还在形成阶段,对于课本中的理论,单凭文字叙述,很难建立起清晰的表象,在学习几何过程中,不妨通过教具来做更好的理解。
2、培养兴趣,兴趣是最好的老师,很多学生在最初遇见数学时是产生极大兴趣的,但是为何后来开始慢慢讨厌数学了呢?很大程度原因是因为挫败感,当学生算错数、做错题了,家长第一反应是批评、责怪,孩子久而久之就开始逃避数学学习了。
3、思维形成,数学问题是错综复杂的,几何更甚。然而,几何的解题方法尤其简单,原因是因为几何是有规定的解题步骤可循的,只要按照解题步骤一步一步做下去,最终都能获得答案。
五、双曲线的实轴和虚轴是什么?
习惯称X轴为实轴,y轴为虚轴。
两顶点之间的线段称为双曲线的实轴,实轴长的一半称为半实轴,实轴的长度为2a(a为标准方程中的参数)。在标准方程中令x=0,得y=-b,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴。
把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a,小于|F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线。
扩展资料:
几何性质:
准线到顶点的距离为Rn/e,准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e大于零时,则P为有限量,准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e等于零时,则P为无限大,P是非普适量。用无限远来定义圆锥曲线是不符合常理的。
教科书中定义局限性的原因是不了解准线的几何性质,当e等于零时则准线为无限远,准线是非普适量,是局限性的量。









