一、4个数字能有多少个四位数的组合?
四个数字组成四位数的组合有24种,
计算方法:4!=4*3*2*1=24个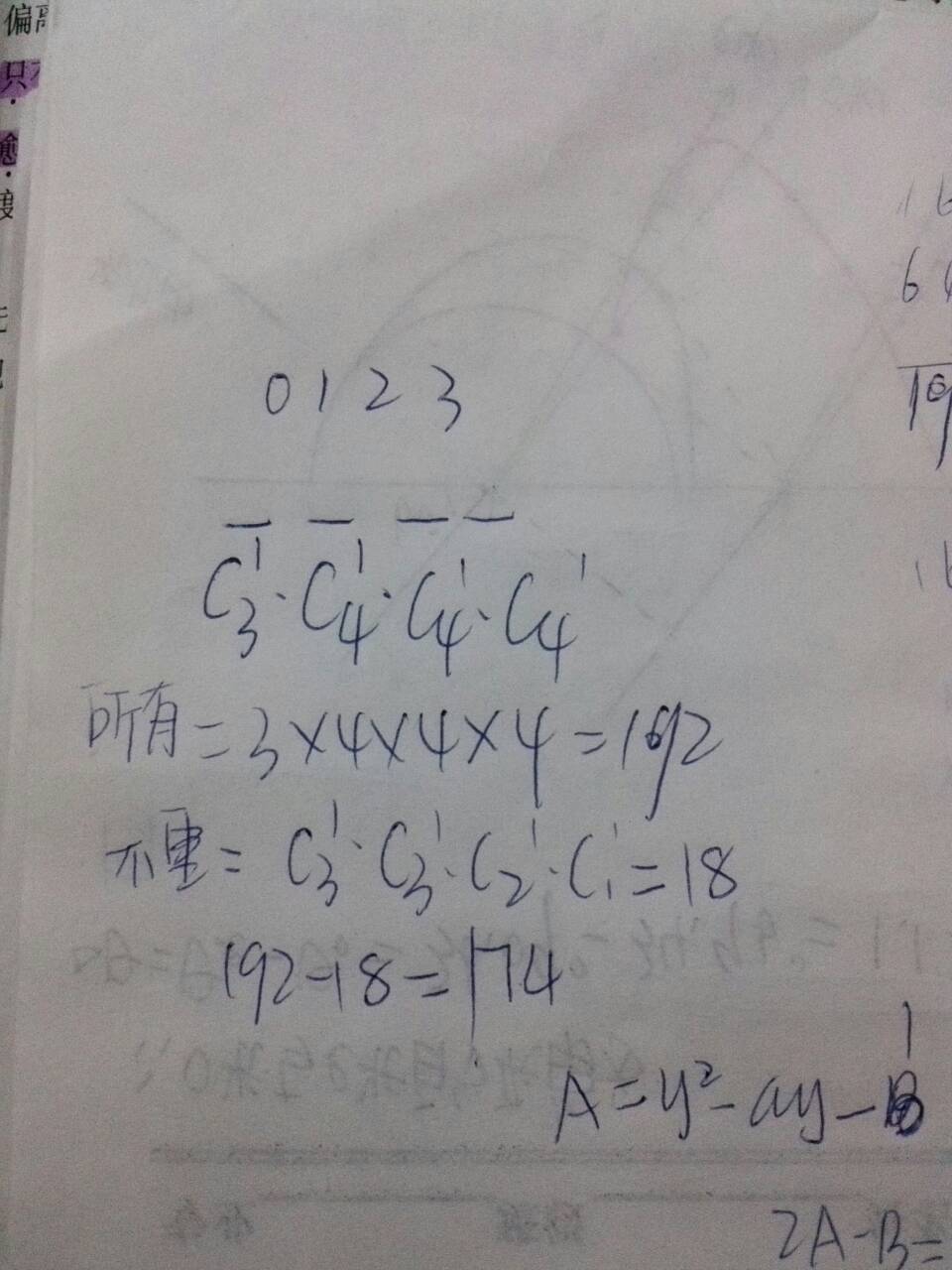
计算有多少种组合可以使用排列组合的方法,
例如2345可以组成24个四位数,这24个四位数分别是:
5234、5243、5324、5342、5432、5423
2534、2543、2354、2345、2453、2435
3524、3542、3245、3254、3425、3452
4325、4352、4235、4253、4523、4532
二、四位数有多少种可能
四位数有9000种可能。
可以通过排列与组合的知识进行说明:
1、四位数是指数字占据了万位、千位、百位、个位四个数位,其中万位的数字不能为9;
2、万位的数字有1-9共9中选择;千位的数字有0-9共10中选择;百位的数字有0-9共10中选择;个位的数字有0-9共10中选择;
3、一共的可能性为:9×10×10×10=9000种。
扩展资料:
两个常用的排列基本计数原理及应用
1、加法原理和分类计数法:
每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不重);完成此任务的任何一种方法,都属于某一类(即分类不漏)。
2、乘法原理和分步计数法:
任何一步的一种方法都不能完成此任务,必须且只须连续完成这n步才能完成此任务;各步计数相互独立;只要有一步中所采取的方法不同,则对应的完成此事的方法也不同。
三、4位数字的排列组合有多少种?
四位数排列组合有24种。
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
公式:
从n个不同元素中,任取m(m≤n,m与n均为自然数,下同)个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。A(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)! 此外规定0!=1。
组合的定义及其计算公式:从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。
用符号 C(n,m) 表示。C(n,m)=A(n,m)∧2/m!=A(n,m)/m!; C(n,m)=C(n,n-m)。(其中n≥m)
四、4个数字有多少种组合?
4个不同的数字有24种排列组合。
可以拿4个不同的数字来进行排列组合,例如2,3,4,5这4个不同的数,当2在最高位时就有2345,2354,2435,2453,2534,2543等6个4位数,那么4个不同的数组成的4位数就有4个6那么多,即24个。
但有一种排列组合比较特珠,也就是随便3个不同的数和0一起排列组合起来的4位数就没有24个了,因为0不能排在最高位上。
排列和组合的区别:
一、意思不同
1、排列:按次序站立或摆放。
例句:哥哥把需要用的参考书排列在桌子上。
2、组合:组织成为整体。
例句:所有这些替代的组合,构成一个补偏救弊的系统。
二、侧重点不同
1、排列:从n个不同的元素中,取r个不重复的元素,按次序排列,称为从n个中取r个的无重复排列。
例句:代表们的名单是按姓氏笔画的顺序排列的。
2、组合:从n个不同的元素中,取r个不重复的元素,组成一个子集,而不考虑其元素的顺序,称为从n个中取r个的无重组和。
例句:台上的这个组合是五位光彩夺目的二八佳人组成的。
















